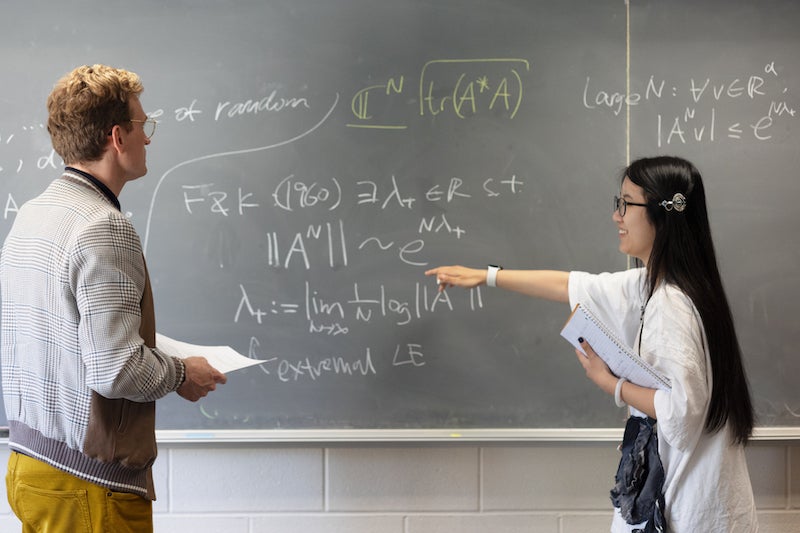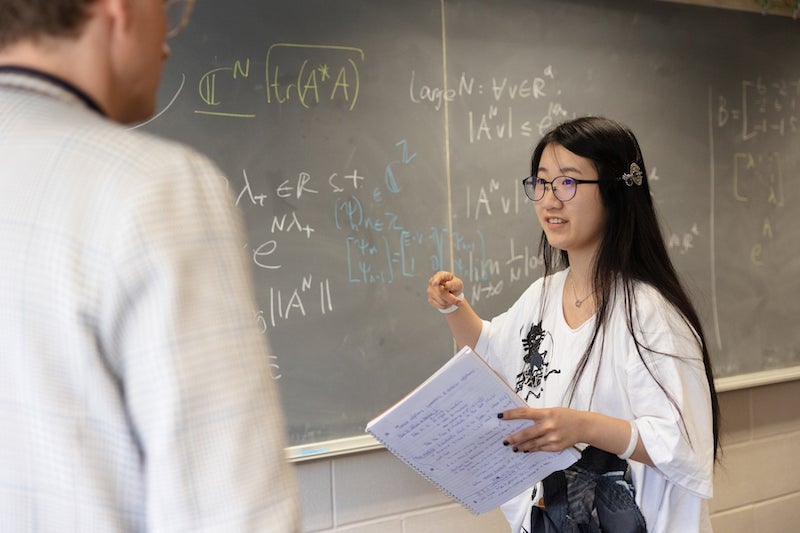The Course that Changed Everything

The class was Math 301: Foundations of Analysis, with Professor Marx. Every math major is required to take it, and it marked an inflection point in the way Zhu experienced math. Instead of what she had been used to—calculations—the focus became proving things: constructing an argument step by step, making it elegant and airtight. The class was tough—the toughest Zhu had ever taken—but that was part of the appeal. “I like complicated and hard, abstract things,” she says.

She also liked that Marx acknowledged how difficult the work was, giving the class permission to get stuck, to get confused, and to wrestle through problems together. “He would encourage us and say, ‘This is how researching math works,’” Zhu recalls.

If this is math research, she thought, this is what I want to do.

The next fall, Zhu returned to Oberlin and began work on an honors thesis with Marx. Her goal was to prepare for graduate school in math—math for its own sake, not as a stepping stone to some other career. That’s when she encountered the sentence that would spark her thesis research:

When n=1, the idea behind the proof is that you integrate the distribution many times until you obtain a continuous function.

The sentence referred to the structure theorem, which forges a key coupling between math and physics. Physicists see the world in terms of change. They have equations to describe the change in the position and direction of a planet, the temperature of a gas particle, the force of an electromagnetic field, and so on. These equations are built on math—a specific tool from calculus called the derivative. 

But derivatives can’t explain all physics fundamentals. For example, to describe the density of a point particle, an infinitely small abstraction that can stand in for real masses and charges, physicists instead use the delta function—a mathematical expression that spikes to infinity at a single point and doesn’t have a derivative. In mathematics, the delta function is also known as a distribution. 

So where does the structure theorem come in? Developed by mathematicians in the middle of the 20th century, this theorem rests on the realization that you can represent distributions using the mathematical opposite of derivatives: integrals. The structure theorem has been proven many times, in many ways, but the comment that caught Zhu’s attention hinted at a completely different way to prove that it works.

The new proof would actually be three different proofs: one for each of three different types of distribution. Zhu found that the approach that worked for the first class of distributions broke down in places when applied to the second—but she found workarounds, and bit by bit, she inched her way through proofs for all three classes. Her work was honored with the Rebecca C. Orr Memorial Prize, awarded annually to a graduating Oberlin mathematics major. She will graduate in December with highest honors in mathematics and plans to study math in graduate school.

She is still fascinated by the deep relationship between math and music. “But now I see it going in a different direction,” she says. After all, in math, there is always more than one way to solve a problem.

As Marx puts it: “There really can be very, very different routes that you can take, and all of these can be correct.”

Kate Becker is a freelance writer based in Massachusetts. She earned a degree in physics from Oberlin in 2001.